En matemáticas, ciencias de la computación y disciplinas relacionadas, un algoritmo (del latín, dixit algorithmus y éste a su vez del matemático persa Al Juarismi) es un conjunto preescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos que no generen dudas a quien lo ejecute. Dados un estado inicial y una entrada, siguiendo los pasos sucesivos se llega a un estado final y se obtiene una solución. Los algoritmos son el objeto de estudio de la algoritmia.
Sobre el Algoritmo ABN
El nombre del algoritmo “ABN” son las iniciales de las características principales del método:
- La “A” de “ABIERTOS”. Es decir, frente al algoritmo tradicional que sólo permite una única forma cerrada a través de la aplicación de instrucciones para resolver los cálculos, este método da libertad a cada alumno/a para que pueda resolverlo de la forma que le sea más cómoda, fácil y comprensible.
- La “BN” de “BASADOS EN NÚMEROS”. Al igual que el tradicional, pero con un tratamiento totalmente diferente y lleno de significación para el alumnado.
En el método tradicional para realizar cuentas (con independencia del número de cifras que tengan cada número o esté formado por unidades, decenas o centenas,..) se actúa sobre cada cifra por separado y se les aplica el mismo tratamiento. Es decir, no importa el lugar que ocupe un cifra, ya sea en las decenas , unidades de millar, .. el proceso es siempre el mismo para cada cifra, con lo cual se pierde el sentido que tienen esas decenas, centenas,…
En el método del algoritmo ABN, el alumno/a trabaja con unidades, decenas, centenas, componiéndolas y descomponiéndolas libremente, para llegar a la solución a través de los pasos que le permita su dominio del cálculo.
Características del método:
- Mejoran el cálculo mental y las estimaciones.
- El alumnado aprende más rápido y mejor.
- Aumenta la capacidad de resolución de problemas.
- Desaparecen ciertas dificultades y trabas del algoritmo tradicional como las llevadas en sumas y restas, la colocación de las cifras, el orden de los términos, las dificultades con los ceros intermedios en la multiplicación, o en la división el cero al cociente intermedio o al final…
- El alumno adapta las operaciones a su nivel de dominio en el cálculo y no es él quien se adapta a la operación.
- Mejora la actitud de los alumnos hacia las matemáticas.
- Afianza la confianza en el cálculo.
En esta secuenciación se establece una descripción de los pasos, una ejemplificación y dos modos de resolución, el cálculo mental y el algoritmo ABN, aunque la secuenciación es igualmente válida para el algoritmo tradicional.
A partir del paso 12, el tipo de sumas que pueden surgir no añaden nada nuevo en el aprendizaje de la suma, pero además no tienen sentido realizarlas con ningún tipo de algoritmo que no sea el de la calculadora, ya que en la vida real no están presentes desdes hace muchísimos años más allá del cálculo mediante el uso de estas ayudas digitales.
Cuando hablamos de realizar las operaciones mediante el cálculo mental, es necesario realizarlo mediante el aprendizaje de la tabla de sumar, la cual puede ser complementada con las primeras series de cálculo mental del método Quinzet, las cuales facilitarán su aprendizaje y afianzamiento.
Bibliografía: “Competencias básicas en matemáticas. Una nueva práctica”. Autor: Jaime Martínez Montero. Editorial Wolters Kluwer España.

Con las explicaciones realizadas en los artículos previos sobre el algoritmo ABN, los ejemplos expuestos y algunas pautas para trabajar la numeración y el cálculo mental, aquellos lectores a los que les haya interesado conocer este algoritmo habrán podido conseguir más información a través de los enlaces que hemos dejado de la página de su creador y de la bibliografía existente hasta el momento.
En este artículo nos centramos en explicar el procedimiento para el algoritmo ABN de la suma. Para ello partimos de varios ejemplos y un vídeo donde una alumna lo realiza en clase.
Para empezar recordar lo que decíamos en el artículo “el algoritmo ABN”: se trata de un procedimiento en el que el alumno lo adapta para realizarlo de la forma que le sea más cómoda. Este principio es muy importante, ya que cuando yo conocí el método, acostumbrado a seguir las reglas del algoritmo tradicional me costaba encontrar la lógica de este nuevo procedimiento. Para hacerlo más comprensivo, los ejemplos que dejo están realizados de tres maneras distintas, aunque pueden ser innumerables, cada una adaptada a cada niño.
Partamos de una suma simple, de las que en el artículo sobre la secuenciación en la introducción de la suma se indica usar este algoritmo. Por ejemplo “decenas incompletas más decenas incompletas” 36 + 43
En primer lugar el alumno/a coloca la suma en la cabecera de una tabla de tres columnas. La primera columna puede representar la cantidad correspondiente al primer sumando que va a ir añadiendo al segundo sumando, en la segunda columna pondrá lo que le quede en el primer sumando, y la última es la suma acumulada de la primera con el segundo sumando. Para simplificar podemos llamar a las columnas respectivamente: “Añado”, “Queda”, “Suma” (El orden de las columnas también puede ser cambiado por el alumno sin que se vea afectada la operación).
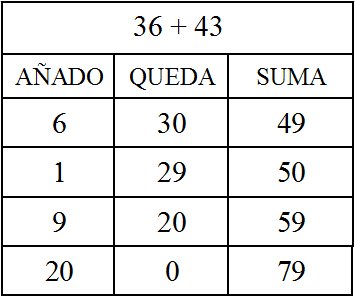
Recordamos nuevamente que los números de la primera columna que corresponden a lo que va tomando el número 36, son elegidos por el niño bajo el criterio de la cantidad que le resulte más fácil ir sumando al 43.
Esta suma se ha resuelto mediante cuatro pasos. Hay que indicar cómo en la segunda línea ha cogido sólo una unidad al objeto de que junto al 49 sume 50 ya que a los alumnos/as por regla general los saltos de una decena a otra les resultan más complicados, por lo que ha optado por formar la decena y continuar la suma.
En el siguiente ejemplo se realiza la misma suma en menos pasos.
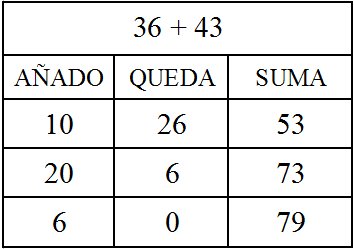
En este caso ha ido directamente con las decenas: primero ha redondeado al 50 y posteriormente ha sumado las 20 restantes, dejando las unidades para el final.
Y por último, con la misma suma, resulta en menos pasos
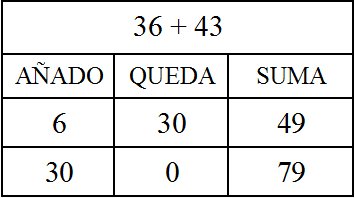
Para ver más sumas realizadas por los propios alumnos y comentadas por su autor puedes ver el artículo “Ejemplos de Sumas ABN“
En el algoritmo tradicional el éxito en la suma depende no sólo de hacer correctamente los cálculos, sino de otros muchos factores que nada tienen que ver con el mismo y que son también fuente de errores. Sin embargo, en el algoritmo ABN el único error posible es el del cálculo en sí. Veamos algunas observaciones al respecto.
1.- Si no somos iguales y cada uno tiene unas dotes de partida distintas, ¿porqué todos deben realizar las operaciones igual, en los mismo número de pasos y de la misma forma? En ABN los pasos que necesita el alumno/a para resolver la operación dependen exclusivamente del dominio del cálculo que dicho alumno/a tenga; por ello un buen adiestramiento en numeración y en la construcción de la tabla de sumar agilizarán y disminuirán los pasos que necesitará para realizar la suma.
2.- Igualmente el orden de realización de los cálculos es indiferente: se puede empezar por decenas, continuar por unidades y acabar por centenas o indistintamente. De esta forma se termina con otro problema que tienen los alumnos al iniciarse en la sumas con llevadas en el algoritmo tradicional. Muchos empiezan por la derecha al igual que hacen a la hora de leer, con lo cual dan al traste con toda la suma.
3.- Desaparecen los problemas derivados del olvido de “me llevo una, dos…” ya que el alumno/a opera con unidades, decenas y en sumas mayores con centenas, o con números completos que contienen diversos órdenes de unidades. Es decir, no sólo suma 20 o 400, sino, por ejemplo, 250 ó 134, según le convenga o la estrategia que el realizador haya adoptado.
4.- Cuando se trata de sumas donde los sumandos tienen distinto número de cifras (245 + 47) desaparece también el problema de no colocar correctamente las unidades debajo de las unidades, las decenas debajo de las decenas,…
5.- En este algoritmo, en cualquier paso del mismo, las operaciones son fácilmente identificables. Podemos decir que estamos vertiendo una cantidad sobre otra y sabemos lo que vertemos, lo que nos queda y lo que acumulamos.
El siguiente vídeo ilustra la realización del cálculo de las suma ABN por una alumna C.E.I.P. Reggio de Puerto Real (Cádiz).
Bibliografía:
“Una nueva didáctica del cálculo para el siglo XXI“. Autor Jaime Martínez Montero (2000). Bilbao: CISS-Praxis.
“Competencias básicas en matemáticas. Una nueva práctica“ Autor Jaime Martínez Montero(2008) Madrid: Wolters Kluwer.
Fuente



No hay comentarios:
Publicar un comentario