El papel de las matemáticas en papel

Origami, escalas, proporciones, etc, etc

Bueno, es evidente que el papel (junto con algo para escribir) ha tenido siempre (es un decir) un papel destacado en las matemáticas. Incluso Claudi Alsina, en su libro Vitaminas matemáticas, incluye la afición de escribir en papelitos como uno de los “tics” de los matemáticos, junto con el despiste parcial, el rigor exagerado, la modesta ambición crematística y la tendencia al asociacionismo.

También es cierto que, junto con la tan querida pizarra, el papel ha tenido siempre (quizás ahora menos, con la aparición de los ordenadores) un lugar de honor en la enseñanza. Sí, cientos y cientos de páginas llenas de letras, números y algún que otro dibujito del profesor bigotudo de química, algún corazoncito o algún “violeta x francisco”. Parece mentira, sin embargo, que este gran recurso no haya sabido aprovecharse como se merece. En este post pretendo rescatar algunas de esas aplicaciones que tan poco entran en las aulas, de matemáticas en este caso, y de las que tanto se puede aprender. En concreto voy a tratar el tema del origami, ya que con el papel se pueden hacer infinidad de cosas y sería demasiado amplio hablar de todas ellas. Para empezar, me gustaría justificar que realmente el origami puede ser una gran ayuda en la educación en general y en las matemáticas en particular. Para ello me baso en los testimonios de personas entendidas en el tema.

Laura Azcoaga nos presenta en este apartado de su página “Origami modular en Argentina” algunas de las habilidades y valores que puede desarrollar el origami:

En la escuela elemental, desde los 6 a los 12 años, el origami es un auxiliar para el desarrollo de varias habilidades esenciales en el proceso educativo:

Perceptivas:
Tamaño y escalas. Utilizando diversas medidas de papel en figuras o modulares.
Composición: combinando elementos de diversa o similar naturaleza para producir efectos complejos.
Transición del plano al espacio: la educación transcurre mayormente en el plano, donde escribimos, dibujamos, etc. Pero el mundo que nos rodea es tridimensional (desde la perspectiva de la geometría clásica). Al plegar el papel agregamos una nueva dimensión a nuestro trabajo.
Lateralidad: en muchas piezas la paridad y la simetría son esenciales y éste no es un tema sencillo. Muchos adultos (yo incluída) tenemos problema con la percepción de las simetrías especulares o de rotación. Ni hablar de la espacial…

Motricidad fina:

La manipulación de papel requiere poder de observación, cuidado por el detalle, diversos grados de fuerza en los pliegues y prolijidad para que los resultados nos complazcan.

Valores individuales y sociales:

Autoestima: una pieza de origami lograda nos llena de satisfacción, para realizarla tuvimos que superar obstáculos, comprender manipulaciones complejas, tolerar la frustración y aplicarnos. Y tiene un efecto sobre los demás… Una vez alguien me preguntó mirando un poliedro que había regalado a un amigo: “¿Y ésto para qué sirve?”. “Por lo pronto, para hacer a dos personas felices: a mí cuando la construí y a mi amigo cuando la recibió”, le contesté. Y sigue siendo cierto con cada pieza que sale de mis manos.

Colaboración y trabajo en equipo: Aún con plegados muy sencillos pueden lograrse efectos espectaculares si todos unen sus esfuerzos en la creación de una obra compleja. Los resultados pueden ser tan atractivos que se destinen a decorar el aula, o la escuela, con el consiguiente incremento de la valoración social del trabajo.

Un estudio más detallado de los beneficios del origami a nivel motor, sensoperceptivo, cognitivo, psicológico y social se puede ver aquí.

En este otro artículo, y ya más relacionado con las matemáticas, se dice del origami:

• Relaciona la disciplina de las matemáticas con otras ciencias, como las artes, por ejemplo.

• Proporciona al profesor de matemáticas una herramienta pedagógica que le permite desarrollar diferentes contenidos, no sólo conceptuales sino de procedimiento.

• También desarrolla la psicomotricidad y, fundamentalmente, la psicomotricidad fina, así como la percepción espacial.

• Desarrolla la destreza manual, la exactitud en la realización del trabajo y la precisión manual.

• Motiva al estudiante a ser creativo, ya que puede desarrollar sus propios modelos e investigar la conexión que tiene con la geometría no sólo plana, sino también espacial.

En “Matemáticas y papiroflexia” se añaden algunas otras ventajas a lo ya dicho:

Dentro del campo de la geometría, fomenta el uso y comprensión de conceptos geométricos, tales como diagonal, mediana, vértice y bisectriz, y la visualización de cuerpos geométricos.

Una vez que el lector ha quedado convencido de los beneficios del origami como recurso educativo (o eso creo), veamos a continuación algunas de sus aplicaciones a la geometría. Para hacer el recorrido más fácil al lector que pasea por esta página haré varios apartados: demostraciones, polígonos, poliedros, otras figuras geométricas (o semigeométricas), materiales interactivos y miscelánea.

Demostraciones:

Se puede decir que la demostración es uno de los pilares básicos de las matemáticas. El origami nos permite realizar bastantes demostraciones para todos los gustos y edades. Para Primaria destaco dos:

• En esta página se demuestra el Teorema de Pitágoras a partir del plegado de papel y basándose en la demostración de Perigal.

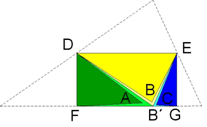
• En este artículo y en esta página aparece una forma sencilla de demostrar que la suma de los ángulos de un triángulo son siempre 180º. Si lo quieres ver de forma interactiva entonces acércate hasta esta otra página.

Pero también hay otras demostraciones más complejas, destinadas a Secundaria:

• Por ejemplo, que arctg1 + arctg2 + arctg3 = π. Alfredo Pérez Giménez nos dice cómo demostrarlo aquí [pdf] y en este otro sitio con un poco más de papiroflexia.

• Demostración de que la diferencia de los cuadrados de dos números es igual al producto de la suma por la diferencia de esos dos números.

Polígonos:

• Un buen estudio a cargo de V. Larios y N. González sobre las posibilidades del papel para aprender los cuadriláteros y su clasificación en Secundaria (y yo diría que también en los últimos años de Primaria, por lo menos siempre que se introduzcan algunas adaptaciones).

• Construcción de polígonos regulares a partir de nudos de papel: J. A. Iranzo nos explica aquí cómo construir un pentágono regular y nos demuestra que realmente es regular. En este otro artículo nos muestra además cómo construir otros polígonos regulares y demuestra que es posible construir cualquier polígono regular, excepto el hexágono, con un nudo (otra cosa es que en la práctica seamos capaces )

• Otra forma de construir polígonos regulares con papel.

• Cómo plegar un heptágono regular.

Poliedros:

Hay que tener en cuenta que los poliedros con papel se pueden construir de muchas formas. Aquí vamos a tratar dos: mediante desarrollos planos (aunque no sea extrictamente papiroflexia) y mediante origami modular. Éste último se basa en la construcción de módulos (piezas de papel) que se ensamblan (la mayoría de las veces sin usar pegamento) para formar cuerpos geométricos o figuras decorativas.

• Aquí dejo una magnífica página llena de desarrollos planos de un montón de poliedros.

• Uno de los artículos que más me gustan es “Origami modular: una oportunidad para estudiar poliedros en secundaria“, de N. González y V. Larios. En él se desarrolla la construcción de los poliedros regulares mediante origami modular y su valor educativo.

• Otra forma de construir los poliedros regulares con origami modular

• Página de Luis López, profesor de Educación Plástica y Visual, en la que se muestra su trabajo con estudiantes de 4º de ESO: poliedros regulares y estrellados.

• Diagramas de diversos poliedros, la mayoría dodecaedros regulares, y otras figuras.

• En Origami modular en Argentina, ya mencionada más arriba, podemos ver una clasificación de módulos y las distintas figuras que se pueden realizar con ellos.

• Y para los que sean más de vídeos, en este post uno [11:05 min] que muestra cómo se construye el módulo Sonobé (uno de los más conocidos) y cómo realizar un cubo y un icosaedro y octaedros estrellados con él.

Hay mucho más sobre este tema, pero creo que con estos enlaces ya hay más que de sobra para que el lector se convierta en un aceptable “origamero poliédrico”.

Otras figuras geométricas (o semigeométricas):

• Cónicas mediante papiroflexia: elipse, hipérbola y parábola.

• Fractales de papel: aquí y aquí.

• Banda de Möbius: no es origami, pero no me resistía a incluirla aquí de todas formas, porque atenta contra la intuición y me parece un recurso muy bueno para las clases de matemáticas. Aplicaciones didácticas aquí (a partir de quinto de Primaria), y aquí

Material interactivo:

Como es lógico, en esta época en la que nos encontramos, también existen recursos interactivos que simulan papeles en los que podemos recortar, plegar… A continuación dos:

• Papiroflexia en hoja rectangular con regla, transportador y compás

• Papiroflexia en hoja triangular con regla, transportador y compás

Miscelánea:

• Y para terminar te dejo el artículo “Construcción de la geometría con materiales diversos“[PDF/ZIP, 256 KB] del apreciado Miguel de Guzmán. Ahí puedes sacar más ideas con papel, por si todo lo anterior no te ha parecido suficiente… En realidad hay mucho, mucho más… y no digamos si nos salimos del mundo de la papiroflexia pero nos quedamos con el papel. No sé, otros aspectos que se pueden tratar con el plegado del papel y que aquí no menciono son determinadas propiedades o características de determinadas figuras geométricas (como los puntos notables del triángulo), conceptos básicos como mediatriz, bisectriz; división de un ángulo o de un segmento en partes iguales…

• [Actualización] En el artículo “Dinamización matemática: jugando con papel y tijeras” [pdf, 333 KB] del nº 14 de la revista Unión se puede ver otra aplicación del papel a las matemáticas, aunque no es origami.

• [Actualización] El capítulo 7 del libro “En el reino del ingenio” también tiene más ideas con papel.

Fuente